2014 Michalski, V., Memisevic, R., Konda, K.
Modeling Deep Temporal Dependencies with Recurrent “Grammar Cells”
Neural Information Processing Systems (NIPS 2014)
[pdf][supplementary][bibtex]
Abstract
We propose modeling time series by representing the transformations that take a frame at time t to a frame at time t+1. To this end we show how a bi-linear model of transformations, such as a gated autoencoder, can be turned into a recurrent network, by training it to predict future frames from the current one and the inferred transformation using backprop-through-time. We also show how stacking multiple layers of gating units in a recurrent pyramid makes it possible to represent the ”syntax” of complicated time series, and that it can outperform standard recurrent neural networks in terms of prediction accuracy on a variety of tasks.
Supplementary Material
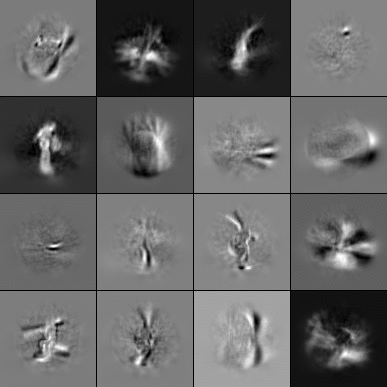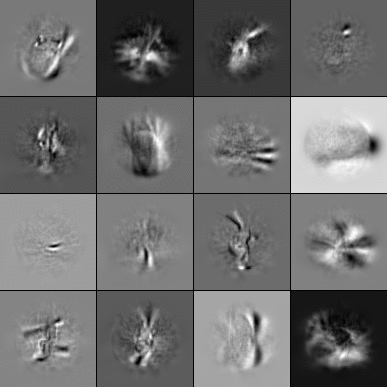
Bottom-layer PGP filter pairs
Filters pairs (left/right input receptive fields) of PGP models trained on the accelerated transformation data sets introduced in our paper, the bouncing balls data set [1] and NORBvideos [2]:
Accelerated Rotations |
Accelerated Shifts |
Bouncing Balls |
NORBvideos |
 |
 |
 |
 |
Generated Sequences
Bouncing Balls
Some sequences generated by a three-layer PGP on the bouncing balls data set (generated with the script released with
(the first 4 frames are seeded, the remaining frames are generated by the model):
Some shorter predicted sequences (right) together with ground truth (left) from preliminary experiments with a 2-layer PGP (3 seed frames not shown):






Chirps
Additional chirp predictions not shown in the paper, because of space restrictions. After seeing 5 windows of 10 frames (frames 1-50) each the models predicted the remaining sequence. The comparison models are the Conditional Restricted Boltzmann Machine (CRBM) [3] trained with contrastive divergence and a vanilla RNN trained with backpropagation through time.
References
[1] I. Sutskever, G. E. Hinton, and G. W. Taylor. The recurrent temporal restricted boltzmann machine. In Advances in Neural Information Processing Systems 21, pages 1601–1608, 2008.
[2] R. Memisevic and G. Exarchakis. Learning invariant features by harnessing the aperture problem. In Proceedings of the 30th International Conference on Machine Learning, 2013.
[3] G. W. Taylor, G. E. Hinton, and S. T. Roweis. Modeling human motion using binary latent variables. In Advances in Neural Information Processing Systems 20, pages 1345–1352, 2007.